2級土木施工管理技士 過去問
令和6年度（後期）
問3 (土木 問3)
問題文
下図の単純梁に集中荷重Pが作用した時に生じる最大の曲げモーメント値Mを求める次の式のうち、正しいものはどれか。
ただし、梁の自重は考慮しないものとする。
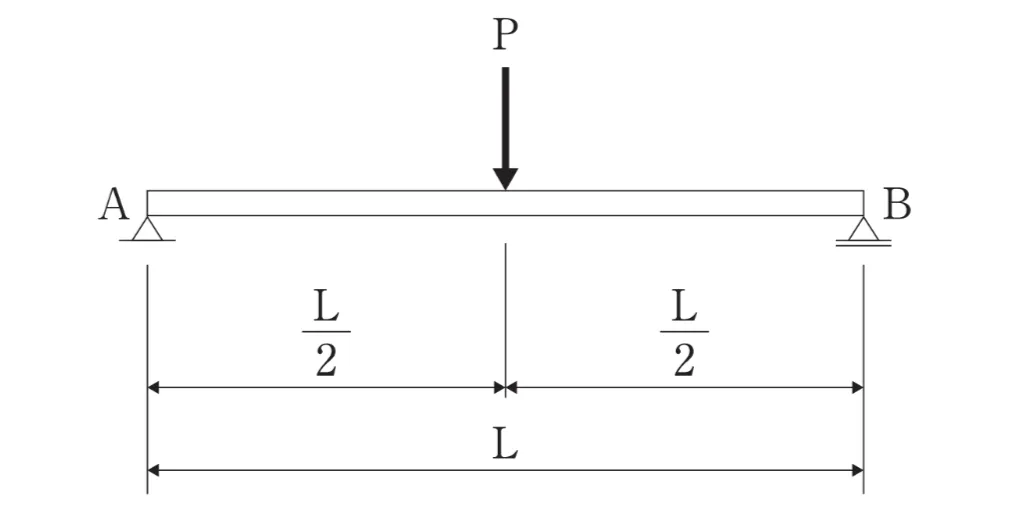
ただし、梁の自重は考慮しないものとする。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
2級土木施工管理技士試験 令和6年度（後期） 問3（土木 問3） （訂正依頼・報告はこちら）
下図の単純梁に集中荷重Pが作用した時に生じる最大の曲げモーメント値Mを求める次の式のうち、正しいものはどれか。
ただし、梁の自重は考慮しないものとする。
ただし、梁の自重は考慮しないものとする。
- M＝PL
- M＝PL／2
- M＝PL／4
- M＝PL／8
正解！素晴らしいです
残念...
この過去問の解説 （2件）
01
この問題は、単純梁の中央に集中荷重が作用した場合に発生する「最大曲げモーメント」を求めるものです。
構造力学の基礎として、反力、せん断力、曲げモーメントの計算手順を理解しているかが問われます。
誤りです。
誤りです。
適当です。
誤りです。
曲げモーメントの計算
曲げモーメントは、ある点から片側を見たときの力のモーメント（力と距離の積）の総和です。
この場合、中央に最大曲げモーメントが発生します。
中央の点C（荷重Pが作用する点）における曲げモーメント$M_{max}$を求めます。
点Cから左側の部分（支点A側）を見て計算します。
左側には、支点Aの反力RAが作用しています。
点Cと支点Aの距離はL/2です。
曲げモーメントは、力と距離を掛け合わせることで求められます。
Mmax=RA×2L
手順1で求めたRA=P/2をこの式に代入します。
Mmax=2P×2L=4PL
以上の計算から、最大曲げモーメントの値はPL/4となります。
参考になった数31
この解説の修正を提案する
02
正しい式は、M＝PL／4です。
単純梁の中央に集中荷重Pがかかるとき、左右の支点反力はそれぞれP／2になり、その反力と荷重の位置関係から、
中央の曲げモーメントが(P／2)×(L／2)=PL／4となります。
支点ではモーメントは0なので、この中央の値が梁の最大曲げモーメントになります。
この式は、反力を考えないで「荷重PがスパンLの端にそのままかかっている」とみなしたような形です。
しかし実際には、支点Aと支点Bが荷重を支えていて、左右にP／2ずつの反力が生じています。
最大曲げモーメントは、反力×距離で求めるので、PLにはなりません。
これも値が大きすぎます。
中央のモーメントは、左半分で考えると、
左支点反力：P／2
その作用点から荷重位置（中央）までの距離：L／2
なので、
曲げモーメントは
M＝(P／2)×(L／2)=PL／4
です。
もしM＝PL／2ならば、上の計算と合いません。
したがって誤りです。
この式が正しいです。
理由を整理すると、次の流れになります。
1.荷重Pが中央にあるので、左右の支点反力は同じ大きさになります。
よって支点反力はそれぞれP／2です。
2.左半分の梁だけを取り出して考えると、左支点反力P／2と、中央の荷重Pがつり合っている状態です。
3.梁の中央での曲げモーメントMは、左支点反力と中央までの距離を使って
M＝(P／2)×(L／2)=PL／4
となります。
4.支点では曲げモーメントは0で、荷重位置（中央）が最も曲げられるので、この値が最大曲げモーメントです。
したがって、M＝PL／4が正しい式です。
これは、先ほど求めた値PL／4のさらに半分になっており、小さすぎます。
支点反力や距離のどちらかを誤って半分にしてしまったような値で、静力学のつり合い条件と合いません。
よって誤りです。
・単純梁の中央に集中荷重Pがかかるとき、左右の支点反力はP／2ずつになります。
・最大曲げモーメントは、荷重位置（ここでは中央）で生じ、
M＝(支点反力)×(支点から荷重までの距離)で求められます。
・この問題では、
支点反力がP／2、距離がL／2なので、
M＝(P／2)×(L／2)=PL／4
が最大曲げモーメントになります。
この基本パターンはよく出題されますので、「単純梁・中央集中荷重→最大曲げモーメントはPL／4」という形でセットで覚えておくと便利です。
参考になった数0
この解説の修正を提案する
前の問題（問2）へ
令和6年度（後期） 問題一覧
次の問題（問4）へ