2級土木施工管理技士 過去問
令和6年度(後期)
問4 (土木 問4)
問題文
ただし、図形の密度及び厚さは均一なものとする。また、図形はイメージである。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
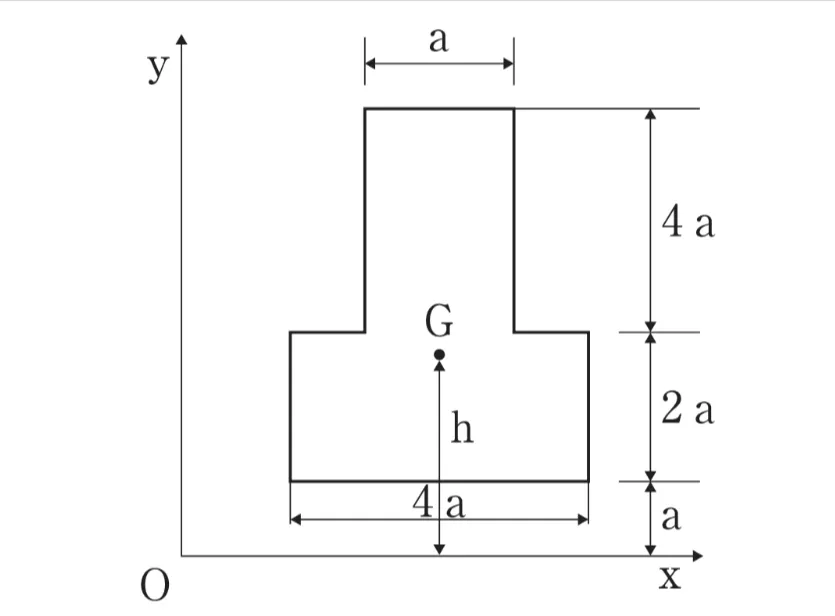
問題
2級土木施工管理技士試験 令和6年度(後期) 問4(土木 問4) (訂正依頼・報告はこちら)
ただし、図形の密度及び厚さは均一なものとする。また、図形はイメージである。

- h=3a/2
- h=2a
- h=5a/2
- h=3a
正解!素晴らしいです
残念...

この過去問の解説 (1件)
01
正しい式は、h=3aです。
逆T型断面を「下の大きな長方形」と「上の細長い長方形」の2つに分けて、それぞれの面積と図心の高さを使って合成することで、全体の図心の高さhを求めると3aになります。
3a/2は、下の長方形だけを考えたときの図心の高さではありません。
図を整理すると、
・下の長方形(幅4a、高さ2a)は、x軸からa〜3aの位置にあります。
→この長方形の図心の高さは
a+2a/2=a+a=2a
・上の細い長方形(幅a、高さ4a)は、x軸から3a〜7aの位置にあります。
→この長方形の図心の高さは
3a+4a/2=3a+2a=5a
これら2つを合わせて全体の図心を求めるので、単純に3a/2にはなりません。
よって誤りです。
これは、下の長方形だけの図心の高さです。
先ほど計算したとおり、下の長方形(幅4a、高さ2a)の図心はx軸から2aの位置にあります。
しかし実際には、その上に細い長方形(幅a、高さ4a)が重なっています。
上の部分にも面積があるので、全体の図心は2aよりも上に移動します。
したがって、h=2aでは足りません。
5a/2は2.5aなので、2aと3aの間の高さです。
ここで、全体の図心の高さhを正しく計算してみます。
・下の長方形
面積A₁=4a×2a=8a²
図心高さy₁=2a
・上の長方形
面積A₂=a×4a=4a²
図心高さy₂=5a
・全体の面積
A=A₁+A₂=8a²+4a²=12a²
・全体の図心の高さh
h=(A₁y₁+A₂y₂)/A
=(8a²×2a+4a²×5a)/12a²
=(16a³+20a³)/12a²
=36a³/12a²
=3a
このように計算すると、5a/2ではなく3aになります。
したがって誤りです。
これが正しい式です。
先ほどの計算のとおり、
・下の長方形:面積8a²、図心高さ2a
・上の長方形:面積4a²、図心高さ5a
を使って合成すると、
h=(8a²×2a+4a²×5a)/(8a²+4a²)
=36a³/12a²
=3a
となります。
図形全体の図心Gは、x軸から3aの高さの位置にあることになります。
・逆T型断面の図心を求めるときは、「いくつかの長方形に分けて考える」のがポイントです。
・それぞれの長方形について
1)面積
2)図心の高さ(ここではx軸からの距離)
を求め、
h=(∑面積×図心高さ)/(∑面積)
の形で計算します。
この問題では、下の幅4a・高さ2aの長方形と、上の幅a・高さ4aの長方形に分けて計算すると、図心Gの高さはh=3aになることがわかります。
こうした「分けてからまとめる」考え方は、他の複合断面の図心計算でもよく使うので、合わせて覚えておくと役に立ちます。
参考になった数0
この解説の修正を提案する
前の問題(問3)へ
令和6年度(後期) 問題一覧
次の問題(問5)へ