2級土木施工管理技士 過去問
令和6年度（後期）
問48 (土木 問48)

誤りです。

誤りです。

正答です。

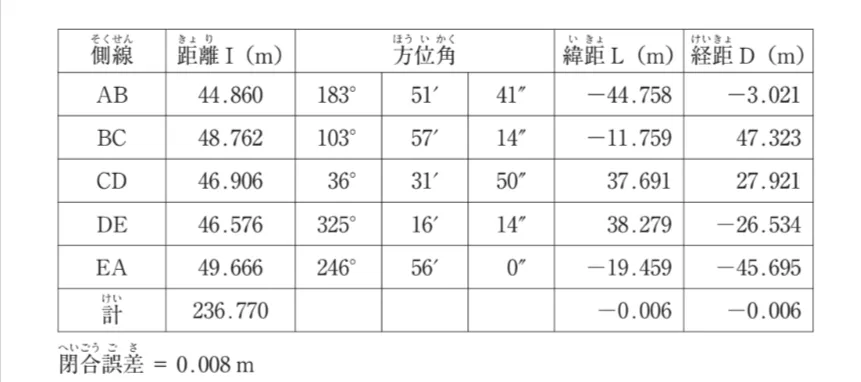
閉合比を計算するためには、まず測線全体の周囲長を求める必要があります。

表中の「距離I」の合計が周囲長であり、その値は236.770mです。

次に、問題文に示されている閉合誤差の値0.008mを使用します。

閉合比は、「閉合誤差」を「周囲長」で割った値の逆数として求められます。

したがって、閉合比は 周囲長閉合誤差​1​ となり、これを計算すると、236.770/0.008＝29596.25なります。

問題文の指示に従い、閉合比の分母を有効数字4桁目を切り捨てて3桁に丸めると、29500となり、閉合比は 1/29500​ となります。

誤りです。

閉合比は、閉合比＝全測線長÷閉合誤差で求めます。

この問題では、表の距離を合計した全測線長が236.770m、閉合誤差が0.008mです。

236.770÷0.008＝29596.25 なので、分母が28100になることはありません。
全測線長を誤って小さく計算したり、閉合誤差の扱いを間違えたときに出てきそうな数字で、正しい値とは言えません。

これも同じ理由で不適切です。
正しい計算では分母は約29600になるので、28300という分母は誤った全測線長や誤った閉合誤差を使って計算した場合に出てしまう数値と考えられます。
したがって、この選択肢も閉合比としては合いません。

この選択肢が正しい閉合比です。

計算の流れを整理すると次の通りです。

表の距離の合計（全測線長）
　Σl＝236.770m

閉合誤差
　E＝0.008m

閉合比R
　R＝Σl／E＝236.770／0.008＝29596.25

「有効数字4桁目を切り捨て、3桁に丸める」という指示に従って
　29596.25 → 有効数字3桁にすると29500

よって、閉合比は1／29500となります。

分母29700は、正しい計算結果29596.25を通常の四捨五入で3桁にしたときに近い値ですが、
問題文では「有効数字4桁目を切り捨て」と明記されています。

つまり、

・四捨五入ではなく
・4桁目を切り落として3桁にする

必要があります。
そのため、29700ではなく29500としなければならず、この選択肢は問題の指示と合いません。