2級土木施工管理技士 過去問
令和7年度（後期）
問48 (土木 問48)
問題文
新点Bの標高を求めるため、新点Bからトータルステーションで既知点Aに設置した反射鏡中心の鉛直角観測と距離測定を行って、下表の観測結果を得た。新点Bの標高として、適当なものは次のうちどれか。
ただし、既知点Aの標高は20.00mとし、AB両点共に偏心はなく、球差と気差を合わせた両差は考慮しないものとする。なお、sin（−30°）＝−0.5
［新点Bにおける観測結果］
高低角 αB −30°00’00″
斜距離 LB 300.00m
既知点Aの測標高 fA 1.40m
新点Bの器械高 iB 1.20m
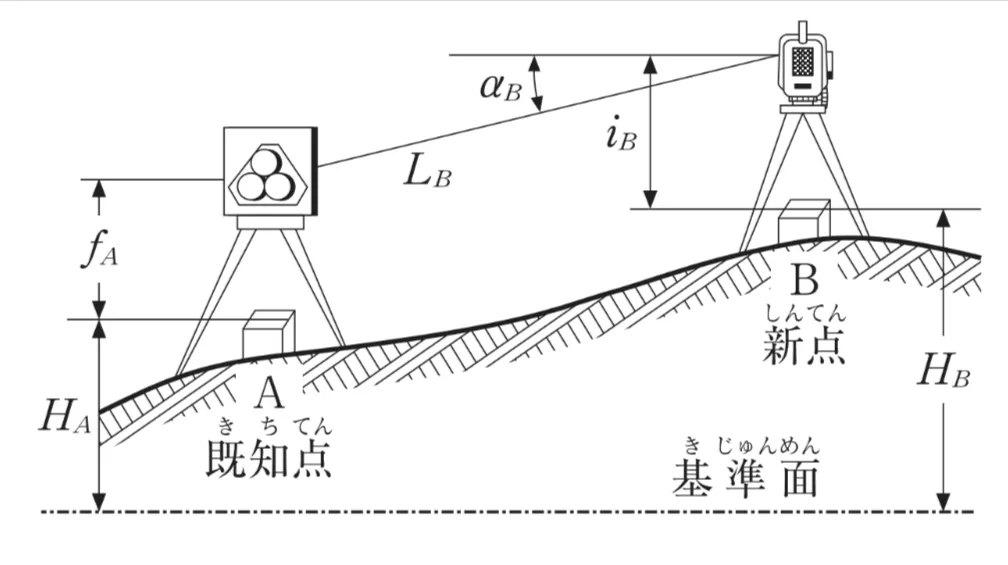
ただし、既知点Aの標高は20.00mとし、AB両点共に偏心はなく、球差と気差を合わせた両差は考慮しないものとする。なお、sin（−30°）＝−0.5
［新点Bにおける観測結果］
高低角 αB −30°00’00″
斜距離 LB 300.00m
既知点Aの測標高 fA 1.40m
新点Bの器械高 iB 1.20m
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する（ここをクリック）」 をご利用ください。
問題
2級土木施工管理技士試験 令和7年度（後期） 問48（土木 問48） （訂正依頼・報告はこちら）
新点Bの標高を求めるため、新点Bからトータルステーションで既知点Aに設置した反射鏡中心の鉛直角観測と距離測定を行って、下表の観測結果を得た。新点Bの標高として、適当なものは次のうちどれか。
ただし、既知点Aの標高は20.00mとし、AB両点共に偏心はなく、球差と気差を合わせた両差は考慮しないものとする。なお、sin（−30°）＝−0.5
［新点Bにおける観測結果］
高低角 αB −30°00’00″
斜距離 LB 300.00m
既知点Aの測標高 fA 1.40m
新点Bの器械高 iB 1.20m
ただし、既知点Aの標高は20.00mとし、AB両点共に偏心はなく、球差と気差を合わせた両差は考慮しないものとする。なお、sin（−30°）＝−0.5
［新点Bにおける観測結果］
高低角 αB −30°00’00″
斜距離 LB 300.00m
既知点Aの測標高 fA 1.40m
新点Bの器械高 iB 1.20m
- 170.20m
- 175.20m
- 180.20m
- 185.20m
正解！素晴らしいです
残念...
この過去問の解説 （1件）
01
新点Bの標高を求める計算式
= 既知点Aの標高 + 器械高(iB) + (斜距離D × sin(高低角α)) - 目標高(fA) ± 両差
今回は両差は考慮しないとされているため、「既知点Aの標高 + 器械高(iB) + (斜距離D × sin(高低角α)) - 目標高(fA)」によって求められます。
設問によって明らかにされている数字をそれぞれに当てはめていきます。
既知点Aの標高 + 器械高(fA) + (斜距離LB × sin(高低角αB)) - 新点Bの器械高(iB)
＝20m＋1.4m＋（300m×sin（－30°））－1.2m
今回、sin（−30°）＝−0.5のため
＝20m＋1.4m＋（300m×0.5）－1.2m
＝21.4m＋150－1.2m
＝170.2m
複雑な計算に見えますが、設問にてsinが指定されているため、整理すれば単純な足し算・引き算の問題です。
ただし計算の仕方を知らなければ求められないため、しっかりと覚えておきましょう。
参考になった数0
この解説の修正を提案する
前の問題（問47）へ
令和7年度（後期） 問題一覧
次の問題（問49）へ