2級土木施工管理技士 過去問
令和7年度(前期)
問48 (土木(ユニットE) 問1)
問題文
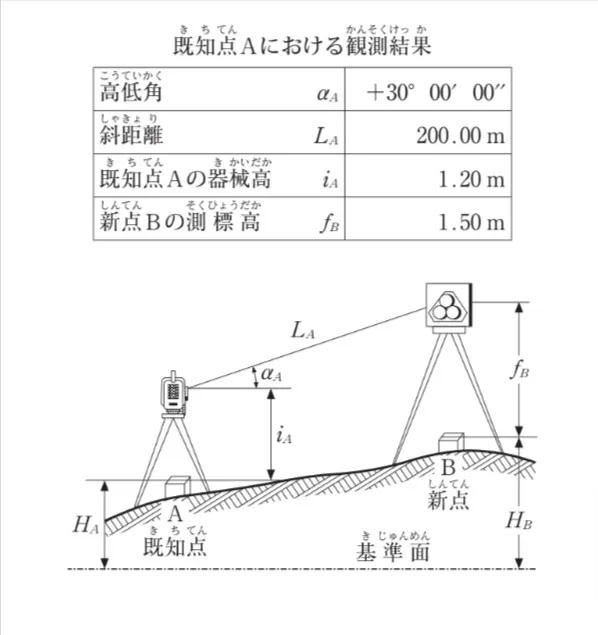
ただし、既知点Aの標高は30.00mとし、AB両点共に偏心はなく、球差と気差を合わせた両差は考慮しないものとする。なお、sin30°=0.5。
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
2級土木施工管理技士試験 令和7年度(前期) 問48(土木(ユニットE) 問1) (訂正依頼・報告はこちら)
ただし、既知点Aの標高は30.00mとし、AB両点共に偏心はなく、球差と気差を合わせた両差は考慮しないものとする。なお、sin30°=0.5。

- 119.70m
- 124.70m
- 129.70m
- 134.70m
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
この問題は、トータルステーションを用いた高低測量に関するもので、観測された高低角と斜距離、および器械高と測標高から新点の標高を計算する基本的な測量計算を問うものです。
測量計算では、観測値から高低差を正確に算出し、既知点の標高に加減することで新点の標高を求めることが重要です。
誤りです。
誤りです。
正答です。
まず高低差 h を計算します。 h=200.00×sin30°=200.00×0.5=100.00 [m]
次に、新点Bの標高 HB を計算します。 HB=30.00+1.20+100.00−1.50=129.70 [m]
したがって、新点Bの標高は129.70mとなります。
誤りです。
この問題のポイントは、高低測量の計算式を正確に理解し、観測値を正しく代入することです。
特に、高低差を求める際に、斜距離と高低角(正弦)を用いること、そして器械高を加算し、測標高を減算することを忘れないようにすることが重要です。
参考になった数31
この解説の修正を提案する
02
この問題では、トータルステーションを用いた測量計算に関する知識を問われています。
既知点Aの標高と、そこから観測して得られた器械高、反射鏡高、斜距離、鉛直角のデータを使って、新点Bの標高を正しく計算できるかがポイントとなります。
誤りです。
誤りです。
適当です。
この問題を解くためには、まず図と表の観測結果を用いて、器械と測標(反射鏡)の中心間の比高(高低差)を計算し、それをもとに新点Bの標高を算出します。
1. 比高(高低差)の計算
器械と測標の間の比高は、斜距離と高低角から求めることができます。
計算式:比高 = 斜距離(LA) × sin(高低角 αA)※今回の問題ではsin30°=0.5
比高 = 200.00m × 0.5 = 100.00m
2. 新点Bの標高(HB)の計算
新点Bの標高は、下記の計算式で求められます。
計算式:新点Bの標高 = 既知点Aの標高 + 器械高 + 比高 - 測標高
新点Bの標高 = 30.00m + 1.20m + 100.00m - 1.50m=129.70m
誤りです。
この問題を解くうえで重要なポイントは、上記の計算式を正しく理解することです。
特に、図をイメージして、どの数値を足して、どの数値を引くのかを混乱しないように注意しましょう。
参考になった数10
この解説の修正を提案する
前の問題(問47)へ
令和7年度(前期) 問題一覧
次の問題(問49)へ